Description

Las exploraciones con Quad2Go son especialmente apropiadas para estudiantes a partir de los 10 años. La enseñanza de la geometría a esta edad suele centrarse en las propiedades de los cuadriláteros y en las relaciones de su estructura de clasificación. Esta perspectiva de aprendizaje entraña distinguir propiedades básicas de rasgos triviales o no definitorios. Esto requiere diferenciar las propiedades clave (las que se pueden encontrar en cualquier ejemplo del concepto: “cuatro lados”, “dos pares de lados paralelos”, o “dos pares ángulos opuestos iguales” son algunas de las determinantes de un paralelogramo) de las no definitorias (como: “dos lados largos y dos cortos” o “dos ángulos agudos y dos obtusos”). En este sentido tal aprendizaje Implica reconocer las propiedades de diversos cuadriláteros, para distinguir las que resultan determinantes de diversos cuadriláteros, y establecer la estructura y jerarquía de clasificación. Quad2Go proporciona diversidad de cuadriláteros aleatorios. Cada ejemplo puede modificarse arrastrando sus vértices o lados.

volver al principio

Características

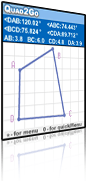
Quad2Go es un recurso portátil que pone a mano, medios para aprender sobre cuadriláteros, produciendo ejemplos, observando y experimentando para avanzar desde la exploración con propósitos particulares a la formulación más general, de conjeturas. Como otros utilitarios (SketchPad Geométrico, Conjeturador- Supposer Geométrico, GeoGebra o Cabri), Quad2Go ofrece un sistema para el tratamiento dinámico de objetos geométricos, útiles para manejarlos, recursos de maniobra e instrumentos de medida. Limitado a cuadriláteros y al marcado de sus diagonales. Quad2Go permite construir, observar y transformar todos los que pueden trazarse con regla y compás, medir lados, ángulos y áreas, y transformar la construcción desplazando, arrastrando y transformando la figura. La figura se modifica al arrastrar alguno de sus elementos que se traslada sobre la pantalla.
El contexto dinámico admite el tratamiento experimental de objetos geométricos acorde al propósito de quien simultáneamente indaga en torno a sus propias acciones y a los resultados, para relacionarlos en un aprendizaje constructivo que parte del reconocimiento causal hacia una lógica de significaciones.

volver al principio

Actividades Sugeridas

Una exploración de la estructura de clasificación de los cuadriláteros:

El menú de figuras permite construir: Paralelogramos, Romboides, Trapezoides y Rombos.

Desde el menú de Quad2Go podemos solicitar paralelogramos.

Frente a cada muestra podemos preguntarnos cómo haríamos para ratificar que estamos frente a un paralelogramo. ¿Qué es lo que controlamos? ¿Cómo? ¿Por qué?

¿Es posible que una de las muestras de paralelogramo resulte un rectángulo?. ¿Un rectángulo, sería una muestra aceptable de paralelogramo? En todo caso, ¿por qué? Si sospecháramos que una de las muestras es un rectángulo, ¿cómo podríamos asegurarlo?

¿Qué categoría del menú de figuras despertaría mayores expectativas de obtener como muestra un cuadrado? ¿Por qué?

Un desafío de exploración en procura de una clasificación poco convencional:

Un cuadrado, un romboide y un rombo son cuadriláteros que tienen en común la siguiente propiedad: son rectos los ángulos comprendidos entre sus diagonales. Acordaremos llamarlos, entonces: “ortodiagonalizados” y nos propondremos inventariar otras propiedades específicas de este tipo de cuadriláteros.

Conocimiento aplicado a triángulos

Se dice que en cualquier cuadrilátero convexo, sendas diagonales delimitan triángulos. Para cada tipo de cuadrilátero nos proponemos identificar:

los 8 triángulos así como los

4 triángulos congruentes; explicando tal decisión

2 triángulos congruentes; explicando tal decisión

Triángulos similares; explicando tal decisión

volver al principio